4: 基于Python的科学计算

Python凭借其简洁的语法和强大的库生态系统，已成为科学计算和数据分析领域首选的编程语言之一。本文档将引导你从基础的数值计算开始，逐步深入到更复杂的科学计算领域，并辅含有可视化的代码示例来帮助理解。

核心库：科学计算的基石

Python的科学计算能力主要构建在几个核心库之上。掌握它们是进行高效科学计算的前提。

  • NumPy (Numerical Python): 提供了多维数组对象（ndarray），以及对这些数组进行操作的各种函数。是几乎所有科学计算库的基础。
  • SciPy (Scientific Python): 基于NumPy，提供了大量用于科学和工程计算的算法，如优化、积分、插值、信号处理、线性代数等。
  • Pandas: 提供了高性能、易于使用的数据结构（如DataFrame）和数据分析工具，特别适合处理结构化数据。
  • Matplotlib: 一个功能强大、灵活的绘图库，可以创建各种静态、动态、交互式的图表。

一、NumPy: 高效的数值计算

NumPy的核心是ndarray对象，它是一个n维数组，可以存储同类型的数据。与Python原生的列表相比，ndarray在数值计算上效率更高，内存占用也更少。

1.1 创建数组

你可以从Python列表或元组创建NumPy数组。

import numpy as np

# 从列表创建一维数组
a = np.array([1, 2, 3, 4, 5])
print(f"1D Array: {a}")
print(f"Shape: {a.shape}")

# 创建一个3x3的二维数组
b = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print("2D Array:\n", b)

# 创建特定类型的数组
c = np.zeros((2, 4))  # 2x4的全零数组
d = np.ones((3, 3), dtype=np.int16) # 3x3的全一整数数组
e = np.arange(0, 10, 2) # 从0到10，步长为2的数组
f = np.linspace(0, 1, 5) # 从0到1，生成5个等间距的数
1D Array: [1 2 3 4 5]
Shape: (5,)
2D Array:
 [[1 2 3]
 [4 5 6]
 [7 8 9]]

1.2 数组运算：向量化

NumPy的强大之处在于其“向量化”运算。你可以在整个数组上执行操作，而无需编写显式的循环，这使得代码更简洁、执行速度更快。

import numpy as np

a = np.array([10, 20, 30, 40])
b = np.array([1, 2, 3, 4])

# 元素级运算
c = a - b  # [ 9 18 27 36]
d = a * b  # [ 10  40  90 160]
e = a**2   # [100 400 900 1600]
f = np.sin(a) # 对每个元素计算正弦值

print(f"a - b = {c}")
print(f"a * b = {d}")

# 矩阵运算
A = np.array([[1, 1], [0, 1]])
B = np.array([[2, 0], [3, 4]])

print("Element-wise product:\n", A * B)
print("Matrix product (dot product):\n", A @ B) # 或者 np.dot(A, B)
a - b = [ 9 18 27 36]
a * b = [ 10  40  90 160]
Element-wise product:
 [[2 0]
 [0 4]]
Matrix product (dot product):
 [[5 4]
 [3 4]]

1.3 索引和切片

NumPy的索引和切片机制非常灵活，与Python列表类似，但功能更强大，支持多维操作。

import numpy as np

arr = np.arange(10) # [0 1 2 3 4 5 6 7 8 9]

# 切片
print(arr[2:5]) # [2 3 4]

# 多维数组索引
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(f"Element at row 1, col 2: {matrix[1, 2]}") # 6

# 切片多维数组
print("First two rows:\n", matrix[:2, :])
print("First column:\n", matrix[:, 0])
[2 3 4]
Element at row 1, col 2: 6
First two rows:
 [[1 2 3]
 [4 5 6]]
First column:
 [1 4 7]

二、SciPy: 科学计算算法库

如果说NumPy是基础的数据结构，那么SciPy就是建立在这个基础之上的算法工具箱。它包含了许多预先构建好、经过优化的函数来解决常见的科学计算问题。

2.1 数值积分 (Numerical Integration)

SciPy的integrate模块可以处理数值积分问题。例如，计算函数 \(f(x) = e^{-x^2}\) 在 \([0, \infty)\) 上的积分。

\[\int_{0}^{\infty} e^{-x^2} dx\]

这个积分的解析解是 \(\frac{\sqrt{\pi}}{2}\)。

import numpy as np
from scipy.integrate import quad

# 定义被积函数
def integrand(x):
    return np.exp(-x**2)

# quad 函数返回两个值：积分结果和估计的误差
result, error = quad(integrand, 0, np.inf)

print(f"Numerical result: {result}")
print(f"Analytical result: {np.sqrt(np.pi) / 2}")
print(f"Estimated error: {error}")
Numerical result: 0.8862269254527579
Analytical result: 0.8862269254527579
Estimated error: 7.101318390472462e-09

2.2 优化 (Optimization)

scipy.optimize 模块提供了一系列函数来寻找函数的最小值或根。例如，我们来寻找函数 \(f(x) = (x-2)^2 + 3\) 的最小值。

from scipy.optimize import minimize

# 定义目标函数
def objective_function(x):
    return (x - 2)**2 + 3

# 使用minimize函数寻找最小值，需要提供一个初始猜测值
# 'BFGS' 是一种常用的优化算法
result = minimize(objective_function, x0=0, method='BFGS')

print(result)
print(f"\nMinimum found at x = {result.x[0]}")
  message: Optimization terminated successfully.
  success: True
   status: 0
      fun: 3.0
        x: [ 2.000e+00]
      nit: 2
      jac: [ 0.000e+00]
 hess_inv: [[ 5.000e-01]]
     nfev: 6
     njev: 3

Minimum found at x = 1.99999998937739

2.3 信号处理 (Signal Processing)

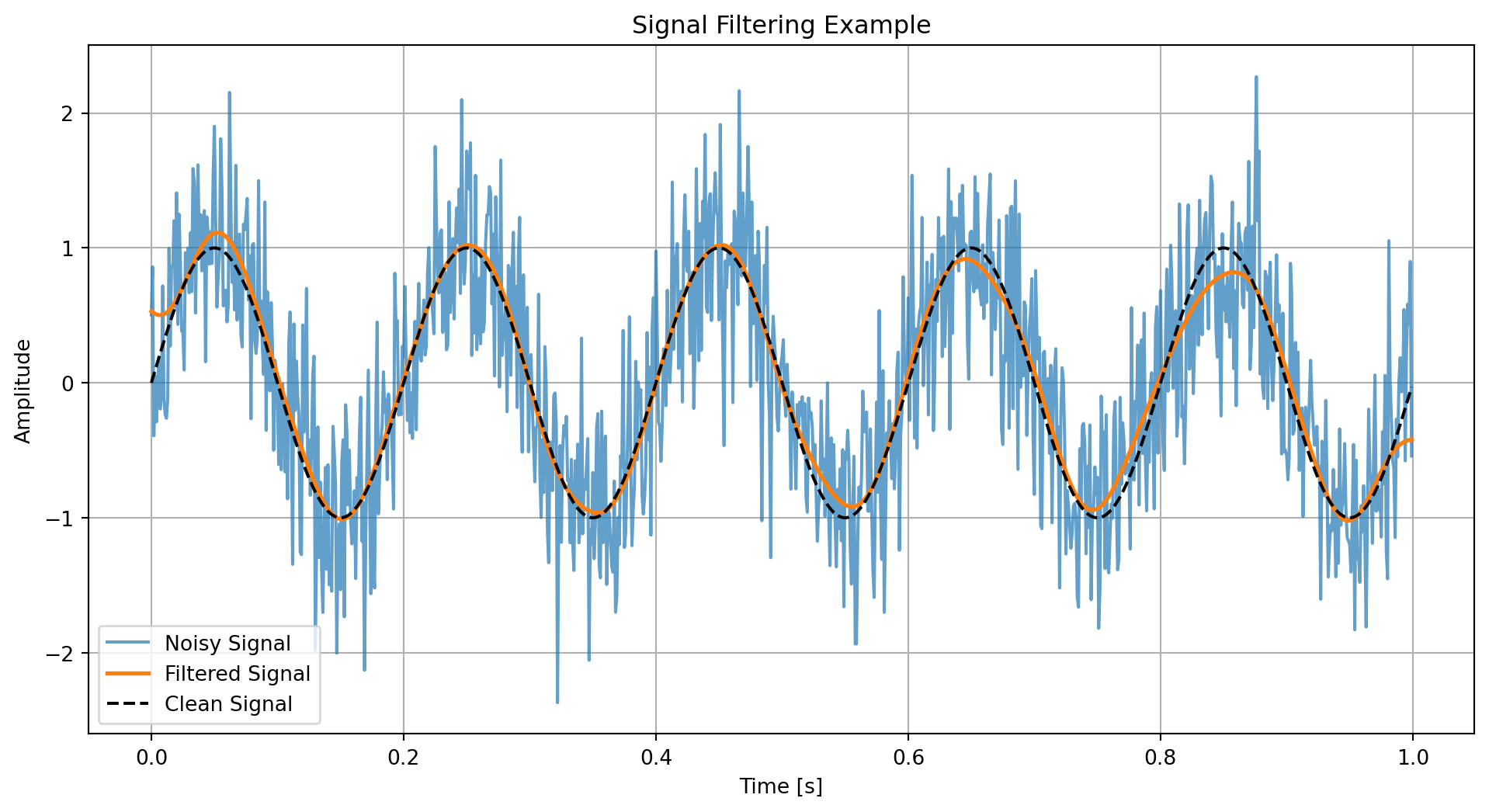
SciPy的signal模块是处理信号的利器。例如，我们可以对一个含有噪声的信号进行滤波。

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 生成信号
t = np.linspace(0, 1, 1000, endpoint=False)
# 一个干净的5Hz正弦波
clean_signal = np.sin(2 * np.pi * 5 * t)
# 添加高斯白噪声
noise = np.random.randn(len(t)) * 0.5
noisy_signal = clean_signal + noise

# 设计一个巴特沃斯低通滤波器
b, a = signal.butter(4, 0.03, 'low') # 4阶，截止频率为0.03

# 应用滤波器
filtered_signal = signal.filtfilt(b, a, noisy_signal)

# 可视化
plt.figure(figsize=(12, 6))
plt.plot(t, noisy_signal, label='Noisy Signal', alpha=0.7)
plt.plot(t, filtered_signal, label='Filtered Signal', linewidth=2)
plt.plot(t, clean_signal, label='Clean Signal', linestyle='--', color='black')
plt.title('Signal Filtering Example')
plt.xlabel('Time [s]')
plt.ylabel('Amplitude')
plt.legend()
plt.grid(True)
plt.show()

三、Pandas: 强大的数据处理

Pandas是处理和分析结构化数据的标准库。它的核心数据结构是Series（一维）和DataFrame（二维），可以让你用直观的方式对数据进行切片、筛选、分组、聚合等操作。

import pandas as pd

# 创建一个DataFrame
data = {
    'Name': ['Alice', 'Bob', 'Charlie', 'David', 'Eva'],
    'Age': [25, 30, 35, 28, 22],
    'City': ['New York', 'Los Angeles', 'Chicago', 'Houston', 'Phoenix'],
    'Salary': [70000, 80000, 90000, 75000, 65000]
}
df = pd.DataFrame(data)

print("Original DataFrame:")
print(df)

# 数据筛选
print("\nPeople older than 30:")
print(df[df['Age'] > 30])

# 分组和聚合
# 按城市计算平均薪水
average_salary_by_city = df.groupby('City')['Salary'].mean()
print("\nAverage salary by city:")
print(average_salary_by_city)
Original DataFrame:
      Name  Age         City  Salary
0    Alice   25     New York   70000
1      Bob   30  Los Angeles   80000
2  Charlie   35      Chicago   90000
3    David   28      Houston   75000
4      Eva   22      Phoenix   65000

People older than 30:
      Name  Age     City  Salary
2  Charlie   35  Chicago   90000

Average salary by city:
City
Chicago        90000.0
Houston        75000.0
Los Angeles    80000.0
New York       70000.0
Phoenix        65000.0
Name: Salary, dtype: float64

四、Matplotlib: 数据可视化

“一图胜千言”。Matplotlib是Python中最基础也最强大的绘图库，能够创建出版质量的图表。

实例：布朗运动与正态分布

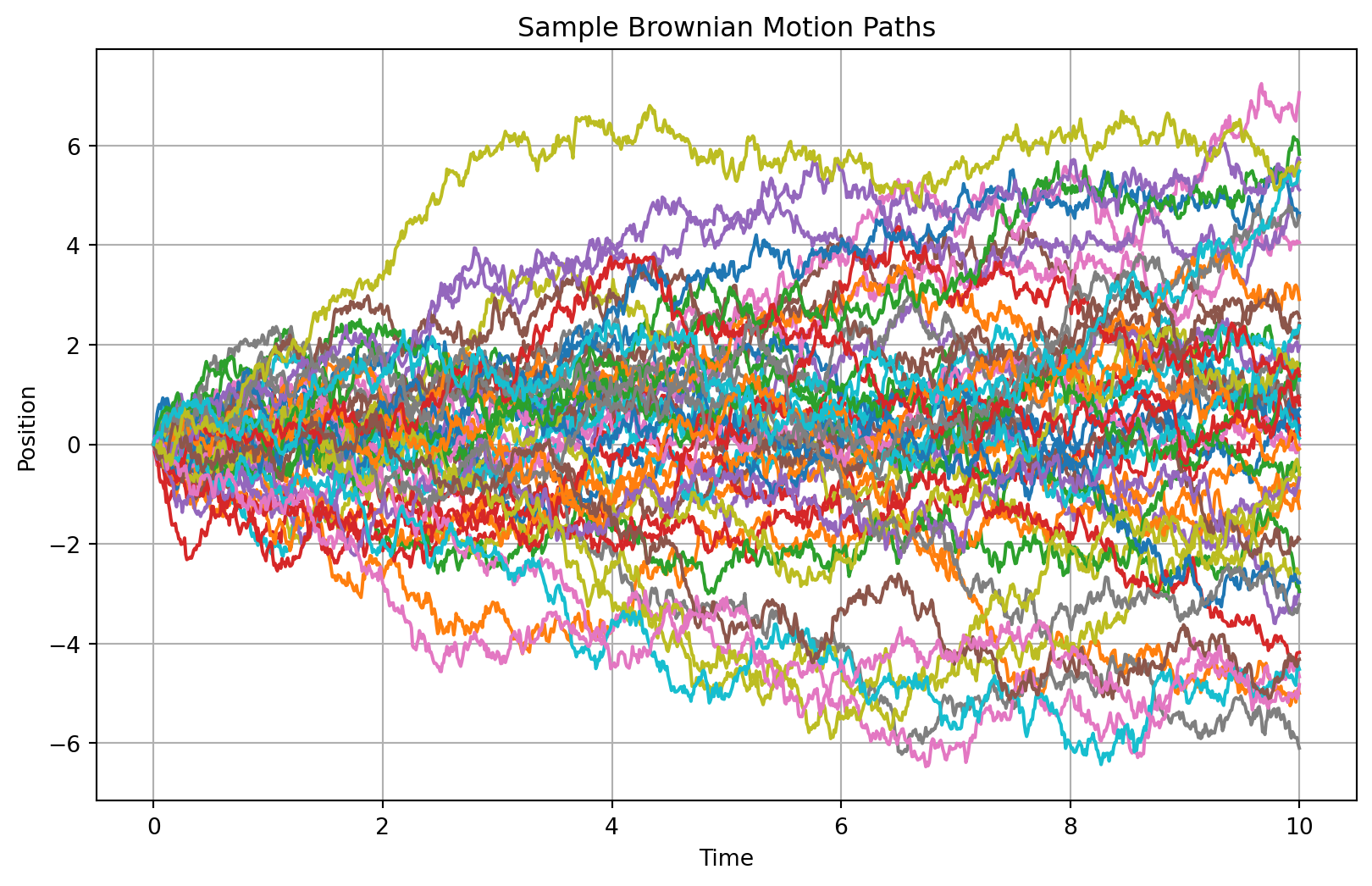
布朗运动（或称维纳过程）是模拟粒子随机游走的数学模型。它与正态分布有着深刻的联系：大量独立粒子经过一段时间的布朗运动后，它们最终位置的分布会趋向于一个正态分布。

这个现象是中心极限定理的一个直观体现。我们可以通过模拟成千上万条独立的布朗运动轨迹来验证这一点。

  1. 模拟过程:
    • 我们模拟 N 个粒子，每个粒子都从原点 (0) 出发。
    • 每个粒子都运动 M 个时间步。
    • 在每个时间步 dt 内，粒子的位移是一个服从正态分布的随机数（均值为0，方差为 dt）。
    • 一个粒子的总位移是所有步位移的累加。
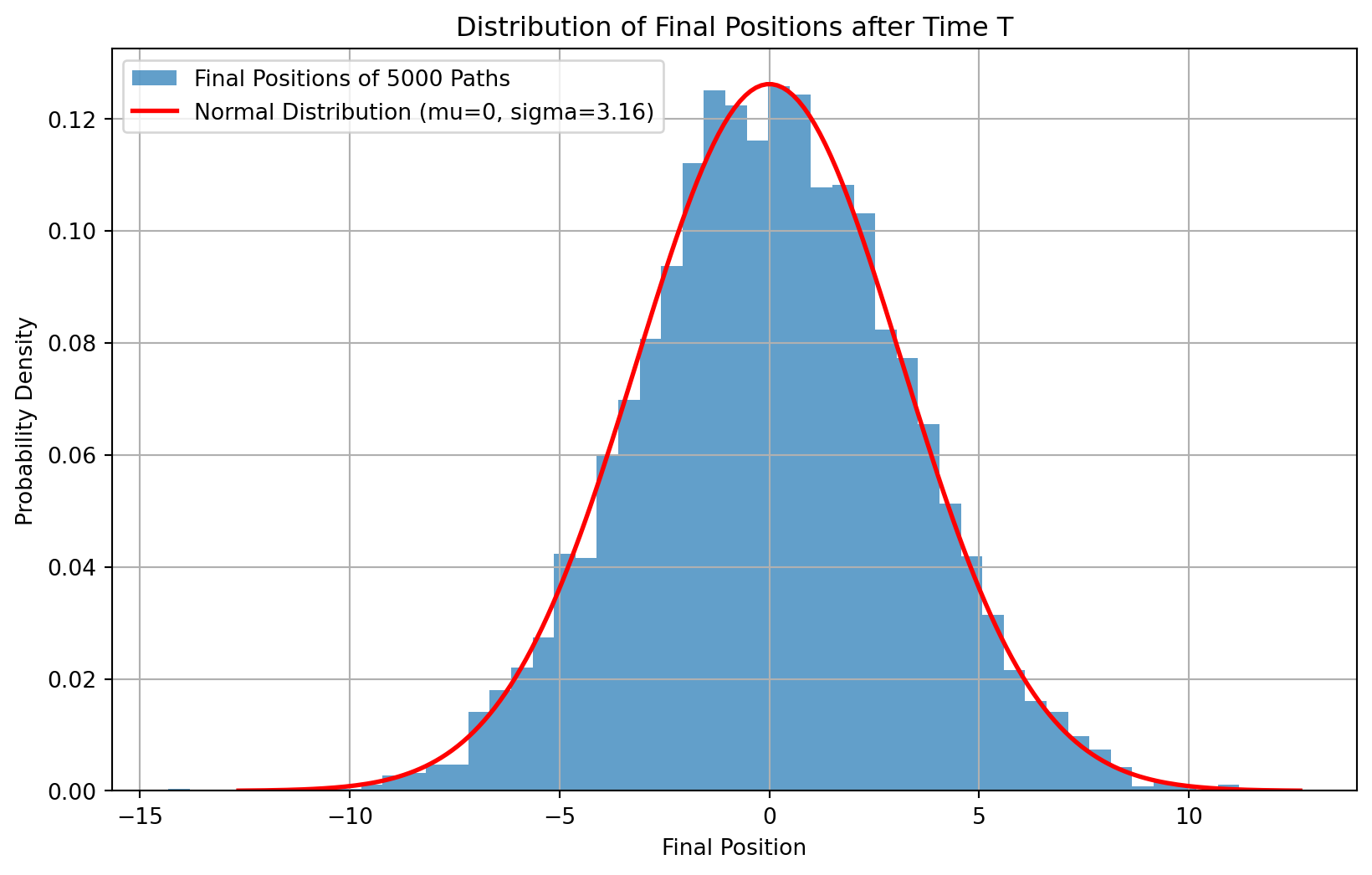
  2. 理论:
    • 根据理论，在总时间 T = M * dt 后，所有粒子最终位置 X(T) 的分布应该是一个均值为 0，方差为 T 的正态分布，即 \(X(T) \sim \mathcal{N}(0, T)\)。

下面的代码将模拟这个过程并进行可视化。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# --- 1. 定义模拟参数 ---
num_paths = 5000  # 模拟的粒子（路径）数量
num_steps = 1000  # 每条路径的时间步数
dt = 0.01         # 每个时间步的长度
T = num_steps * dt # 总时间

# --- 2. 生成布朗运动路径 ---
# 为每条路径的每一步生成一个随机位移
# 位移服从均值为0, 标准差为sqrt(dt)的正态分布
random_steps = np.random.normal(0, np.sqrt(dt), (num_paths, num_steps))

# 计算每条路径在每个时间点的位置
# 使用cumsum(axis=1)对时间步进行累加
# 在开头插入0，表示所有路径都从0开始
initial_positions = np.zeros((num_paths, 1))
paths = np.concatenate((initial_positions, random_steps), axis=1)
paths = np.cumsum(paths, axis=1)

# 创建时间轴
time_axis = np.linspace(0, T, num_steps + 1)

# --- 3. 可视化部分 ---

# 图1：展示几条样本路径
plt.figure(figsize=(10, 6))
# 只画前50条路径，否则会很乱
for i in range(50):
    plt.plot(time_axis, paths[i, :])

plt.title('Sample Brownian Motion Paths')
plt.xlabel('Time')
plt.ylabel('Position')
plt.grid(True)
plt.show()

final_positions = paths[:, -1]

# 计算理论上的正态分布参数
mu = 0
sigma = np.sqrt(T)

# 创建用于绘制理论曲线的x轴
x_theory = np.linspace(mu - 4*sigma, mu + 4*sigma, 200)
# 计算理论正态分布的概率密度函数 (PDF)
pdf_theory = norm.pdf(x_theory, loc=mu, scale=sigma)

plt.figure(figsize=(10, 6))

# 绘制最终位置的直方图
# density=True 表示将直方图面积归一化，以便与PDF比较
plt.hist(final_positions, bins=50, density=True, alpha=0.7, label=f'Final Positions of {num_paths} Paths')

# 叠加理论上的正态分布曲线
plt.plot(x_theory, pdf_theory, 'r-', lw=2, label=f'Normal Distribution (mu=0, sigma={sigma:.2f})')

plt.title('Distribution of Final Positions after Time T')
plt.xlabel('Final Position')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()

结果分析: 第一张图展示了粒子随机游走的轨迹。第二张图是核心，它清晰地显示了5000个粒子在运动10秒后，其最终位置的分布（蓝色直方图）与理论上的正态分布曲线（红色）完美吻合。这直观地证明了布朗运动与正态分布之间的深刻联系。

五、进阶话题：符号计算与机器学习

5.1 SymPy: 符号计算

与NumPy和SciPy进行数值计算不同，SymPy可以进行符号计算（代数运算）。这意味着你可以处理数学表达式，而不是数值。

import sympy as sp

# 定义符号
x, y = sp.symbols('x y')

# 创建表达式
expr = (x + y)**2
print(f"Original expression: {expr}")

# 展开表达式
expanded_expr = sp.expand(expr)
print(f"Expanded expression: {expanded_expr}") # x**2 + 2*x*y + y**2

# 对表达式求导
derivative_expr = sp.diff(expanded_expr, x)
print(f"Derivative with respect to x: {derivative_expr}") # 2*x + 2*y

# 解方程 x**2 - 4 = 0
solutions = sp.solve(x**2 - 4, x)
print(f"Solutions for x**2 - 4 = 0 are: {solutions}") # [-2, 2]
Original expression: (x + y)**2
Expanded expression: x**2 + 2*x*y + y**2
Derivative with respect to x: 2*x + 2*y
Solutions for x**2 - 4 = 0 are: [-2, 2]

5.2 Scikit-learn: 机器学习

Scikit-learn是建立在NumPy, SciPy和Matplotlib之上的机器学习库，提供了大量易于使用的监督学习和无监督学习算法。

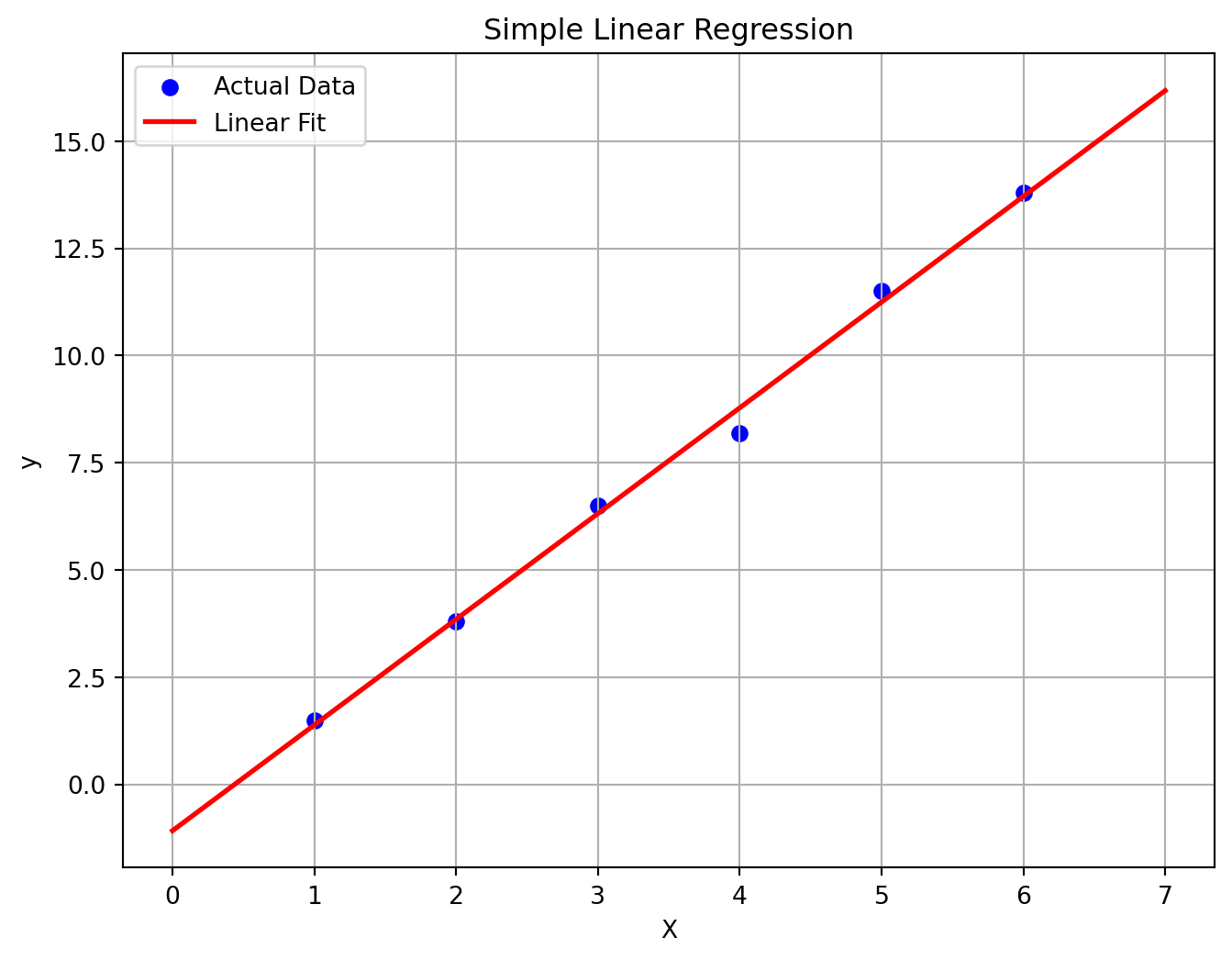
这里是一个简单的线性回归示例。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 创建一些样本数据
# X 必须是二维数组
X = np.array([[1], [2], [3], [4], [5], [6]])
y = np.array([1.5, 3.8, 6.5, 8.2, 11.5, 13.8])

# 创建并训练模型
model = LinearRegression()
model.fit(X, y)

# 预测
X_new = np.array([[0], [7]])
y_pred = model.predict(X_new)

# 打印模型参数
print(f"Intercept: {model.intercept_}") # 截距
print(f"Coefficient: {model.coef_[0]}") # 斜率

# 可视化结果
plt.figure(figsize=(8, 6))
plt.scatter(X, y, color='blue', label='Actual Data')
plt.plot(X_new, y_pred, color='red', linewidth=2, label='Linear Fit')
plt.title('Simple Linear Regression')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()
Intercept: -1.080000000000001
Coefficient: 2.4657142857142857

结论

Python通过其强大的科学计算库生态系统，为研究人员、工程师和数据科学家提供了一套完整、高效且易于上手的工具。从基础的数组操作到复杂的机器学习模型，你都可以在Python中找到解决方案。希望本文档能为你开启Python科学计算的大门。继续探索，不断实践，你将能利用Python解决更多有趣的实际问题。